catrel

CATEGORICAL RELATIONSHIPS

Given any two categories, there exists at least three and no more than four possible categorical relationships between them:

separate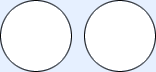	intersecting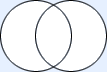	hierarchical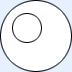
No members of one are members of the other.	Some members of each are contained, and not contained in the other.	One is contained in the other.

If you want to count two identical categories as two categories, then "identical" is a fourth possible categorical relationship. You can also treat identical categories as one category. It usually depends on whether they are definitionally identical or coincidentally identical.

definitionally identical: (all bachelors) (all unmarried men)
These categories are always identical.

coincidentally identical: (all girls in the room) (all blonds in the room)
These categories are identical relative to a particular place at a particular time, but not necessarily always identical.

There are at least three kinds of hierarchical relationships. The contained set is either a subset, a part, or a subordinate of the container set. e.g.

Hondas and Fords are subsets of cars.
Engines and tires are parts of cars.
Lieutenants and sergeants are subordinates of captains.

Sets may be categorized in at least three ways: e.g.

1. by the number of concepts in them
A null set contains no concepts.

A finite set contains at least one concept, and may include any number of concepts short of infinity.

A unitary set is a subset of finite sets containing only one concept.

An infinite set contains an infinite number of concepts.

If it is unknown whether a given set contains a finite or infinite number of concepts, that set should be called a set of unknown finitude, rather than a potentially infinite set. A potentially infinite set cannot be shown to exist or not exist.

2. by the criteria their members have in common
a. by the number of criteria their members have in common

Singular sets have one criterion in common
Composite sets have more than one criterion in common

b. by the type of criteria their members have in common
Simple sets have one type of criteria in common
Complex sets have more than one type of criteria in common

3. by the clarity of their boundaries
Distinct sets have clear boundaries
Vague sets have at least one unclear boundary.

But still there exist some concepts which are definitely in the set, and some concepts which are definitely outside the set.

There are, of course, degrees of clarity.

Concepts may be categorized by boundary.
Distinct concepts have clear boundaries.
Vague concepts have at least one unclear boundary.

Boundless concepts have neither boundaries nor places for boundaries to be.
e.g. zero, emptiness, vacuum, nothing, absence, point

Bounded concepts have at least one boundary, and are therefore either totally finite, partly finite, or infinite.

Totally finite concepts have boundaries on all sides.

Partly finite concepts have at least one bounded side, and at least one open side. e.g. time & space, divisibility & multiplicity

Note that infinity in one dimension does not imply infinity in more than one dimension.
e.g. Space is infinite in three dimensions (assuming either an infinite universe, or an infinite number of universes in one space continuum)
A plane is infinite in only two dimensions.
A line is infinite in only one dimension, but two directions.
A direction is finite on one end and infinite on the other.

Totally infinite concepts (if they exist) have only open dimensions.
e.g. everything, anything, existence
Paradoxically however, infinity becomes a limit in itself.

Therefore all bounded concepts exist in degrees and types of finiteness.